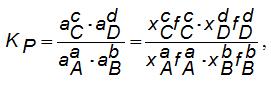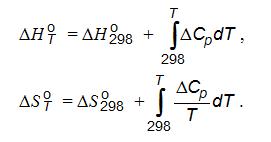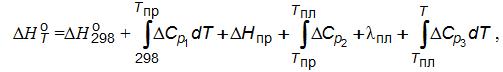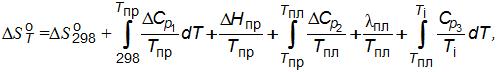1.1. Термохимия ферросплавных процессов

Содержание > Глава 1. Физико-химические основы ферросплавных процессов > 1.1. Термохимия ферросплавных процессов

Ферросплавные процессы основываются на законах физической химии, а конкретнее — на законах химической термодинамики (термохимии)и химической кинетики (термокинетики). Законы химической термодинамики при помощи математического аппарата позволяют решать задачи и получать ответы на вопросы: может ли та или иная реакция протекать при конкретных заданных параметрах процесса (температуре Т и давлении Р) и, если может, то в каком направлении она будет идти. Таким образом, законы химической термодинамики решают задачу о возможности и направленности химической реакции при заданных параметрах процесса. Законы химической кинетики дают возможность оценить по известным аналитическим связям время, в течении которого данная реакция при изменившихся параметрах процесса (Т, Р) может из неравновесной перейти в равновесное состояние.
Термохимия это раздел химической термодинамики в приложении к высокотемпературным химическим (металлургическим) процессам. Возможность и направленность реакций в термохимических процессах определяется термодинамической величиной – изменением энергии Гиббса (∆G ):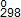

для стандартного состояния (Т = 298 K, Р = 101,3 кПа) функция ∆G 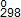имеет вид прямой у = b – kx;
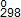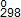∆G  = ∆Н  – Т∆S 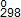, где ∆Н  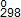– изменение энтальпии, а ∆S 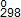- изменение энтропии реакции.
Входящие в эту формулу величины имеют следующую размерность: ∆G 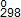 – Дж/моль; ∆Н  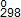– Дж/моль;∆S 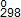– Дж/(моль К); Т – K.
Ферросплавный процесс с участием многокомпонентных шихтовых материалов может быть сведен к однойопределяющей цель и задачу технологического процесса реакции, которая запишется в следующем виде:

аА + bВ ↔ сС + dD±∆Н.

Константа равновесия (KР*)реакции, являющаяся математическим выражением закона действующих масс, имеет вид:

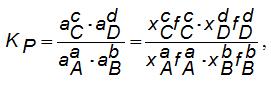
где а – активности участвующих в реакции компонентов; х – мольные доли соответствующего компонента; f– коэффициенты активности этих компонентов.
При температурах ферросплавных процессов возможность и направленность реакций оценивают по величине ∆G = ∆Н - ∆S×T.
Аналитическое исследование функции ∆G(Т)свидетельствует, что величина ∆G может принимать три значения: 1) ∆G < 0; 2) ∆G > 0; 3) ∆G= 0. В физической химии принято, что если ∆G <0, реакция для заданных условий (Т, Р) протекает в прямом направлении (т.е. в сторону образования продуктов реакции); если ∆G > 0, — реакция, если она находилась в равновесии, при изменении Т, Р должна смещаться в сторону исходных компонентов и, если ∆G = 0, — реакция находится в равновесии. В учебной, а иногда и в научной литературе, весьма часто условия ∆G > 0 интерпретируется не совсем корректно. Указывается, что при этом условии исходные компоненты реакции не будут взаимодействовать. Следует иметь в виду, что при ∆G > 0 и определенных параметрах (Т, Р) реакция может протекать, однако выход продуктов реакции будет не полный; если же реакция находилась в равнове- сии, а условия изменились так, что величина ∆G стала больше нуля, то реакция сместится в сторону исходных компонентов и выход продуктов реакции уменьшится.

В теории электрометаллургических (ферросплавных) процессов, температуру, соответствующую условию ∆G= 0, принимают за температуру начала химической реакции, хотя, как указано выше, реакция и при условии ∆G> 0 может протекать, но с меньшим выходом продуктов, чем при условии ∆G< 0.
Поскольку ∆Gи константа равновесия реакции KР взаимосвязаны соотношением:

∆G= – RT ln KР,

условия ∆G< 0 соответствуют KР > 1; ∆G> 0, KР< 1 и ∆G= 0 при KР = 1.
Для большинства индивидуальных веществ и химических реакций, протекающих в ферросплавных процессах, термодинамические функции приведены для стандартных условий. В реальных условиях эти процессы протекают при высоких и весьма высоких температурах. При полном описании термодинамики реакций рассчитывают величину ∆G(Т) для любой заданной высокой температуры. Для этого предварительно рассчитывают ∆Н(Т)и ∆S(Т):

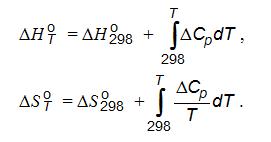
Многие компоненты, участвующие в реакциях ферросплавных процессов, испытывают фазовые превращения, сопровождающиеся изменением их кристаллохимических структур и агрегатного состояния. Эти превращения сопряжены с изменением энергии в реагирующих системах, которая должно учитываться в более точных термодинамических расчетах ∆Н(Т)и ∆S(Т)по приведенным ниже формулам:

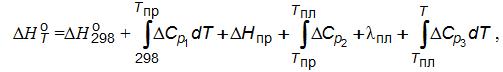
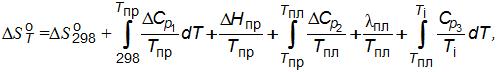
где ∆СР – изменение теплоемкости веществ, Дж/(моль K; ∆Нпри lпл – энтальпия превращения компонентов и теплота плавления веществ, соответственно.
Возможность и направленность реакции можно оценивать по величине константы равновесия. Условие KР= 1 соответствует равновесию реакции, KР > 1 – реакция протекает в сторону образования продуктов реакции и KР< 1 – выход продуктов реакции снижается.
Поскольку ∆G= –RTlnKР = ∆Н– ∆SТ, то lnKР, = –∆Н/RT +∆S/RT; обозначив –∆Н/R= –А и ∆S/R= В, получают зависимость KР(T)(формулу Аррениуса):

lnKР= –А/Т + В.

Таким образом, константа равновесия реакции зависит от температуры (при постоянном давлении) и не зависит от активности (концентрации) участвующих в реакции компонентов. При наличии в системе конденсированных и газообразных компонентов константы равновесия есть функции температуры и давления.
В ферросплавных процессах реакции могут быть эндотермическими (углеродотермические процессы с участием твердого углерода) и экзотермическими (металлотермические процессы). В некоторых случаях важно оценить влияние температуры (давления) на направленность реакции. Оценку внешнего воздействия можно производить используя теорему (принцип) Ле-Шателье: “Если нарушить условия системы, находившейся в равновесии, то в системе стремится протекать такая реакция, которая противодействует произошедшему нарушению, т.е. реакция, частично уничтожает эффект нарушения”.
В соответствии с уравнением Вант-Гоффа константа равновесия связана с изменением энтальпии реакции изобарой

∆Н = RT2(dlnKР)/dT).

Количественное выражение теоремы Ле-Шателье дается уравнением Клаузиуса-Клапейрона

dР/dT = Q/T∆V,

где dР/dТ –  изменение давления при изменении температуры Т; Q – теплота поглощения или выделяемая граммом вещества; ∆V – изменение удельного объема, сопровождающее реакции.

______________
* Константа равновесия реакции может быть безразмерной величиной (когда все входящие величины выражены через активности) или иметь размерность, если наряду сактивностями входят величины парциальных давлений некоторых компонентов, например K= аSi∙р2CO.