Содержание > ГЛАВА 2. Ффазовые равновесия в металлических и оксидных ферросплавных системах> 2.3 Трехкомпонентные диаграммы фазовых равновесий

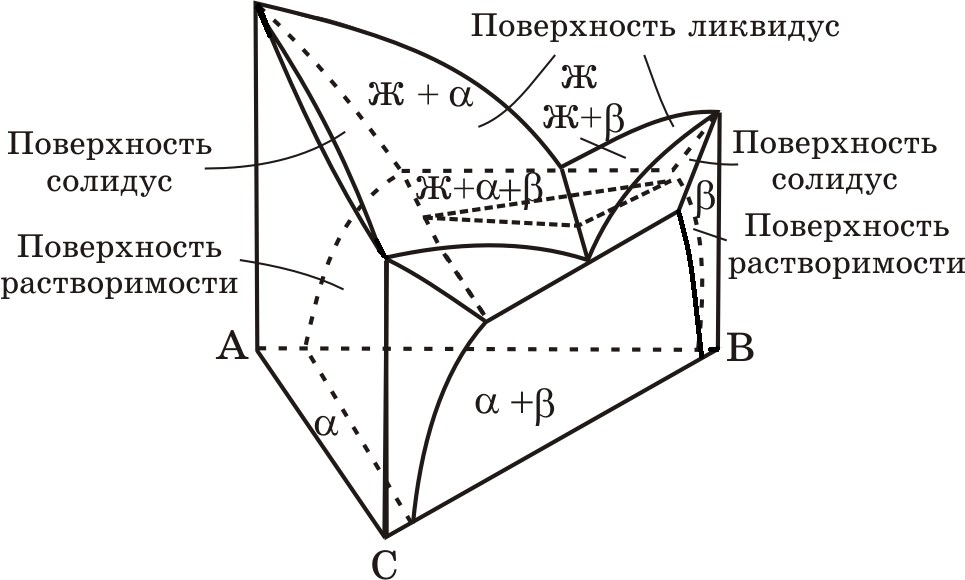
Диаграмма Х – Т системы, состоящей из трех компонентов, графически изображается объемно так, что на горизонтальной плоскости наносится состав, а по вертикали — температура. Трехфазное равновесие на пространственной модели для двух эвтектических и одной изоморфной бинарных систем представлено на рис. 2.9.

Рис. 2.9. Трехфазное равновесие в простой тройной системе

На пространственном изображении равновесия фаз в системе МnО–FеО–SiO₂ (рис. 2.10)пунктирной линией показана область существования двух несмешивающихся жидкостей. Для изображения фазовых равновесий в тройной конденсированной системе используют треугольник Гиббса. Чистые компоненты (100%) находятся по вершинам треугольника, двойные составы по его сторонам, а тройные — внутри треугольника. Тригональную призму можно рассекать горизонтальными или вертикальными плоскостями и получать изотермическое или изоплетное* (политермное) сечение на плоскости.

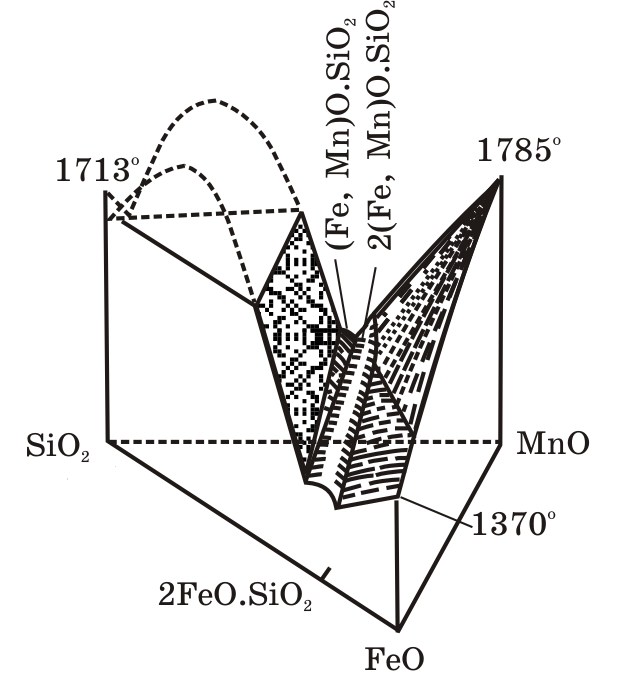
Рис. 2.10.Пространственная модель состояния системы MnO–FeO–SiO₂

Для расчета состава сплава, находящегося внутри треугольника, необходимо через заданную точку провести три линии, параллельные его сторонам. Отрезки прямых линий, отсекаемые точкой пересечения их и удаленные от вершины треугольника (содержания чистых компонентов), будут характеризовать процентное содержание каждого компонента в тройном сплаве.
Многокомпонентные системы. Диаграммы фазовых равновесий систем, содержащих четыре и более компонентов, весьма сложны. Так, диаграмма температура — состав для четырехкомпонентной системы потребовала бы четырех измерений. Поэтому используют изобарические или изоплетные сечения. Для нахождения состава в четырехкомпонентной системе используют правильный тетраэдр, обладающий теми же свойствами, что иравносторонний треугольник.
Суммарная длина отрезков прямых, проведенных через заданную точку параллельно четырем ребрам до пересечения с соответствующими гранями, равна длине любого ребра, принятого за 100%.
Конодные треугольники. Для характеристики трехфазного равновесия на диаграмме необходимо применение такого элемента диаграммы, который при каждой выбранной температуре показывал бы состав трех сопряженных фаз. Таким элементом по Ф. Райнзу является треугольник, составленный из конод (рис. 2.11.).

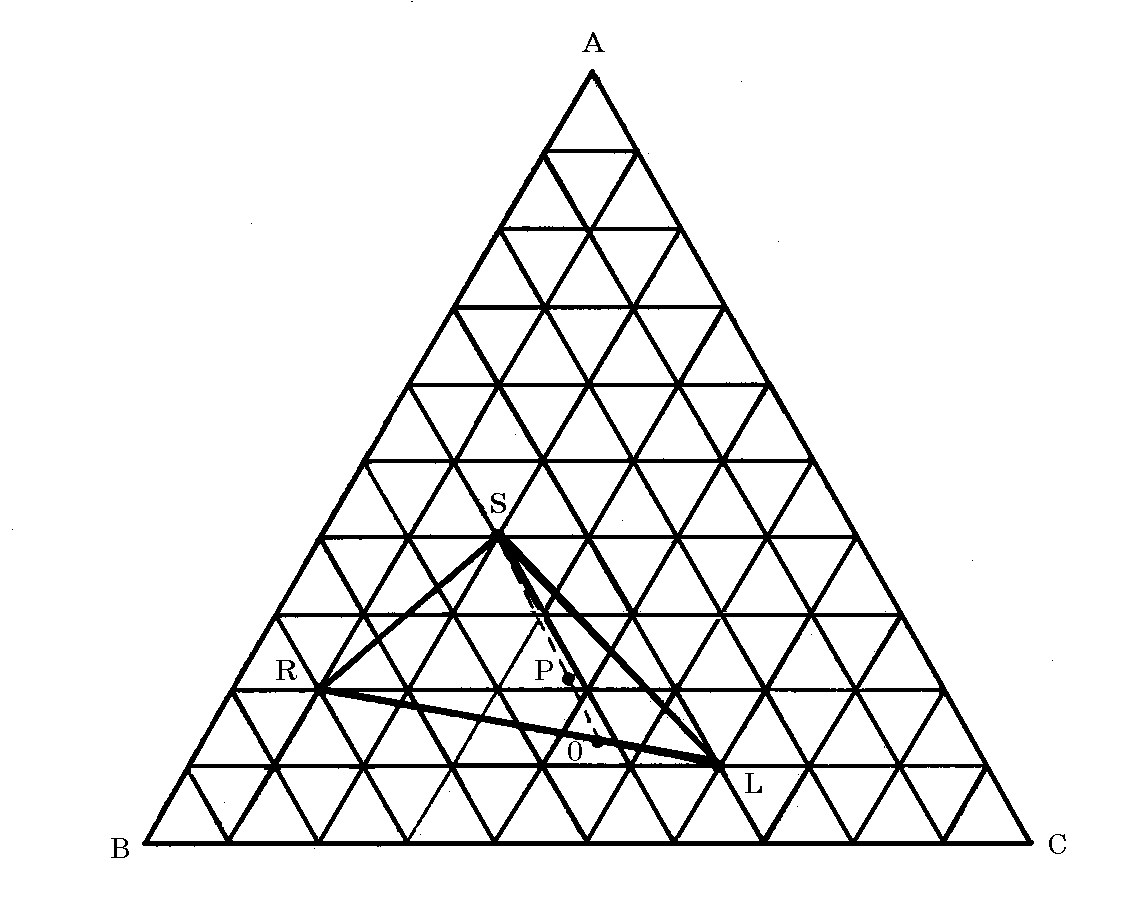
Рис.2. 11. Анализ конодного треугольника

При смешении любых трех трехкомпонентных сплавов состав образованного нового сплава Р будет находиться внутри треугольника RSL. Пример расчета состава сплава Р. Известно три состава R, S и L (рис.2. 11):

R = 20%A + 70%B + 10%C;
S = 40%A + 40%B + 20%C;
L = 10%A + 30%B + 60%C.

При смешении двух частей сплава состава R с тремя частями сплава S и пятью частями сплава L получаем состав сплава Р:

0,2х20 + 0,3х40 + 0,5х10 = 21%А
0,2х70 + 0,3х40 + 0,5х30 = 41%В
0,2х10 + 0,3х20 +0,5х60 = 38%С

Итак состав сплава Р (21%А + 41%В + 38%С) будет находиться внутри треугольника RLS, в точке Р (рис. 2.11). Правило конодного треугольника остается верным независимо от того, в какой пропорции были взяты три сплава составов R, S и L.

________________
*Изоплета – вертикальное сечение диаграммы фазовых равновесий